When exoplanets pass in front of their host star (as seen from Earth), a portion of the start light is blocked out and a decrease in the photon flux is measured. Measuring the change in flux over time, allows for the creation of a light curve. Fitting models to the light curve, various characteristics such as orbital motions and atmospheric composition can be extracted. Both the size of the host star and the planet will determine the decrease in flux during the transit. The orbital distance between the exoplanet and its host star does not affect the transit depth due to the enormous distance from Earth.
The transit method is particularly useful for calculating the radius of an exoplanet. To first order (assuming the stellar disc is of uniform brightness, and neglecting any flux from the planet) the ratio of the observed change in flux, , to that of the stellar flux
can be expressed as:
where and
are the planetary and stellar radii respectively. As described below, limb-darkening will have an affect on the transit light curve, but to first order, the equation above holds.
Impact Parameter:
The total transit duration is heavily dependent on the impact parameter , which is defined as the sky-projected distance between the centre of the stellar disc and the centre of the planetary disc at conjunction* and is shown in Fig. 1**. Assuming a circular orbit the impact parameter is expressed as:
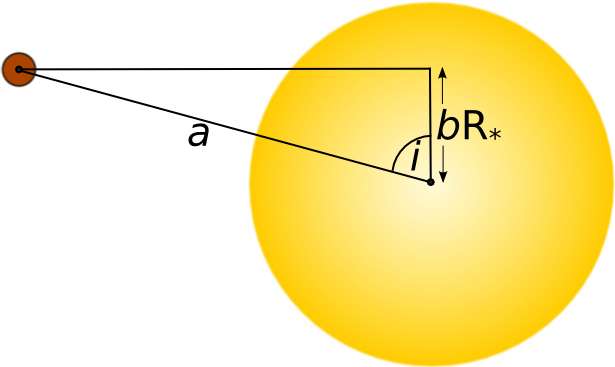
Fig. 1: The impact parameter varies from
centre of stellar disk with
being on the cusp of the disc.
Transit Duration:
The total transit duration, , defined as the time during which any part of the planet obscures the disc of the star, depends on how the planet transits the host star. If the exoplanet crosses the centre of the stellar disc (
), the transit duration is the longest with
signifying a shorter transit duration. With the help of Fig. 2 and using Pythagoras’s theorem, the length the planet has to travel across the disk of the star can be expressed as,

Fig. 2: Star-planet geometry showing the distance traversed by the planet, , impact parameter of the system,
and the stellar and planetary radii,
and
respectively.
With the aid of Fig. 3, the exoplanet moves from to
around its orbit, creating an angle
(measured in radians) with respect to the centre of the host star.
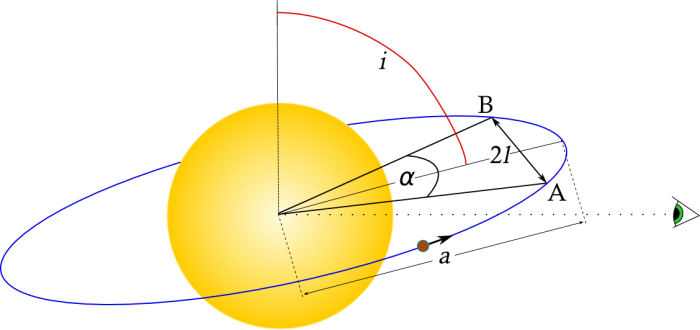
Fig. 3: The orbital geometry of a transiting exoplanet system showing the projected distance travelled across the surface of the star, , between the points
to
and the angle
this geometry forms, with the inclination,
, and semi major axis,
, shown.
With the assumption of a circular orbit, the distance around an entire orbit is , where a is the radius of the orbit. The arclength between points
and
is
and the distance along a straight line between
and
is
.
From the triangle formed by ,
and the centre of the star,
thus
an expression of the full transit duration.
The Effects of Limb Darkening:
The effect caused by the stellar disk being brighter in the centre compared to the limb of the disk is called limb darkening. Photons emitted from the limb of the stellar disc at a certain atmospheric depth , follow a more oblique path through the stellar atmosphere compared to the photons emitted from the centre of the stellar disc as seen in Fig. 4. For the photons escaping the edge of the stellar disc, an optical depth of unity is reached at a higher altitude where the temperature is cooler (
) and the radiation is less intense causing the apparent darkening.
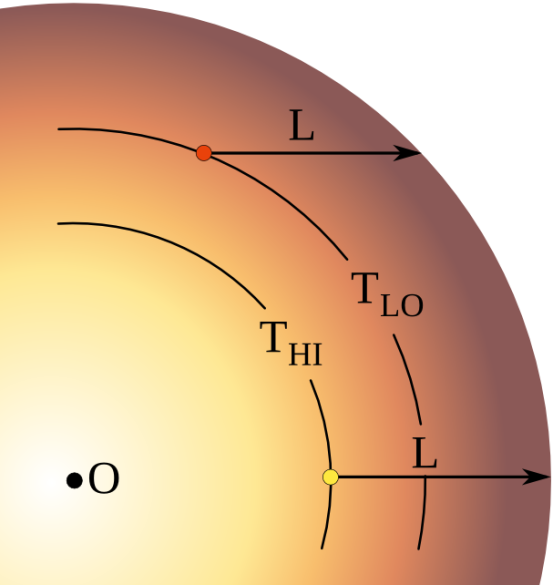
Fig. 4: Limb darkening of a star showing how the intensity and temperature diminishes as an observer looks towards the limb of the star.
The limb darkening effect is largest at short wavelengths where a highly rounded light curve is observed. For longer wavelengths the effect is less severe and the centre of the transit takes on a flatter shape (see Fig. 5).
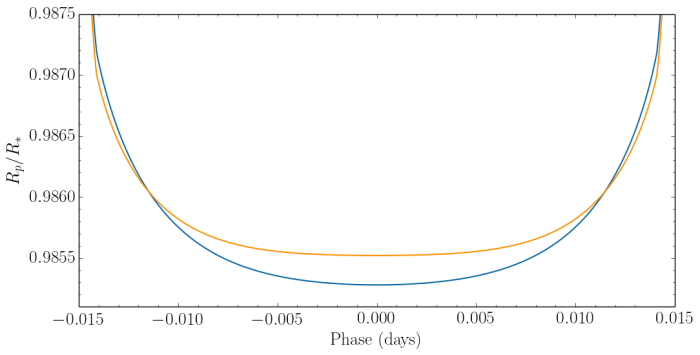
Fig. 5: Two model light curves of the super-Earth GJ~1214b for observations at 5000 Å (blue) and (orange) using a tunable filter with a width of 12 Å. Observations at shorter wavelengths result in a deeper and narrower transit.
Orbital Inclination:
Radial velocity observations provide information about the minimum mass, of , assuming the stellar mass is known. To constrain the actual mass of an exoplanet, the orbital inclination,
, has to be measured. This is done by fitting a analytical transit light curve to the data using the transit equation of \cite{mandel02}. A transiting exoplanet which has an impact parameter
or
, will have a shorter transit duration, a shallower transit depth and longer ingress and egress times. This is seen in Fig. 6 where the effects of varying
from
to
is shown.
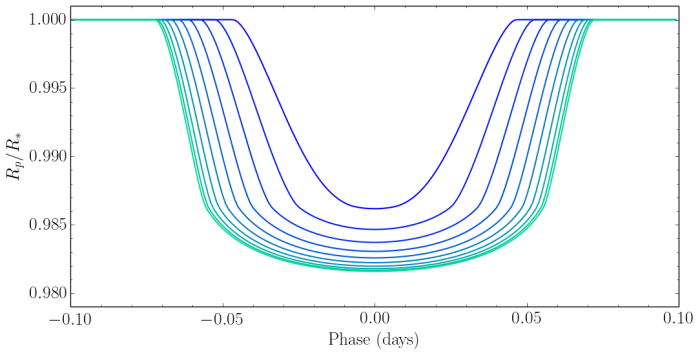
Fig. 6: Inclination values ranging from to
at
intervals, with the shallowest light curve corresponding to
.
* Conjunction: The point in the orbit where two objects are most closely aligned, as viewed from Earth
** The figures and derivations are adapted from “Transiting Exoplanets”, by Carole A. Haswell.
62 Comments
Leave a Comment

Does the variable P refer to the orbital period here?
Yes it does.
Is there any method to calculate the orbital inclination from it?
Hi Paul,
Firstly many thanks for your blog. It’s quite interesting!
I’ve a request regarding the topic “Orbital inclination”. I’ve noticed that the reference to the transit equation is missing. Please, could you provide it? I’d like to know more about it.
Many thanks,
Roque
Hi Roque.
Have a look at the book: “Transiting Exoplanets”, by Carole A. Haswell.
Alternatively have a look at this paper by Joshua Winn: https://arxiv.org/pdf/1001.2010v5.pdf which is an excellent resource.
whats the first equation called?
Not sure it has a name. It is simply a ratio of fluxes where the flux is expressed as: F = L / 4*pi*R^2 (the inverse square law, where L is luminosity).
Is it possible to replace flux with lux ? Or are they just the same.
In astronomy the flux term is commonly defined as the amount of energy transferred in the form of photons at a certain distance from the source per unit area per second. Check out Radiative flux. Lux is similar in that it also measures a flux per unit area, however, lux is used as a measure of the intensity, as perceived by the human eye. Since we are interested in the total loss of flux and not just the loss of flux perceived by the human eye, we choose to not use lux but flux.
Hello! Sorry for my off-the-wall amateur questions.
First off, I couldn’t find a definition of “transit depth”. Is it basically an amount of the “dip” in the star’s brightness?
Is the “transit depth” roughly proportional to the ratio of the planet’s disk area to the star’s disk area? TD ≈ ((Rp)^2) / ((R*)^2) ?
The reason I’m asking – I was looking at one of the many discussions about the famous Tabby’s star’s 20% dips in brightness, and according to Wiki, the leading theory is a “swarm of comets”. One of the papers Wiki ( https://en.wikipedia.org/wiki/KIC_8462852 ) refers to ( https://arxiv.org/abs/1511.08821 ), says “To reach a transit depth of ∼0.2, the comets need to be in a close group of ∼30, if they are ∼100 km in radius”. I can’t see how this could be: Tabby’s star radius is 1.58 of our Sun, or about 1000000km, so if my understanding of the “transit depth” is correct, TD of such a swarm should be 0.0000002, not 0.2. Am I missing something basic?
Thank you so much!
Boris
Hi Boris.
When we are talking about transit depth we are referring to how much flux has been blocked out compared to some reference. Usually the reference is the continuum (basically when nothing is transiting in front of the star). Say then that the star is transited by an exoplanet, comet etc.. then this will cause a decrease in the measured flux and we will see a dip in the light curve. The difference in flux from the continuum to the lowest point of the light curve is what we call the transit depth. Typically hot Jupiters block out 1-2 % percent of the flux. This is equivalent to a transit depth of 0.01 – 0.02.
Tabby’s star is an extraordinary case where a lot more light is being blocked out at times. A transit depth of 0.2 means that 20% of the flux is being blocked out. Have a look at Fig 1. from the paper you are referring to. They have normalised the flux so that 1 is their reference. Then the transit event occurs and they measure 0.8. This means a 1 – 0.8 = 0.2 transit depth = 20% decrease.
(An update to my previous comment)
Found what I was missing: I read the paper itself rather than just the abstract, and it’s not the comets themselves that are supposed to cause the dip in brightness, but rather, the clouds of dust they produce when grazing the star. They assume a very high dust-production rate and large groups of comets, all grazing the star simultaneously.
Thank you so much!
Boris
That is correct Boris. The comets are tiny in comparison with the star and block out a negligible amount of light. It is what they leave behind such as dust which blocks the light. Good on you for continuing to read the paper!
Hey Paul.
Im a student and i wondered if you could help me calculate the radius of an exoplanet.
I know you touched it in the first part of the text, but i wondered if you could go into a little bit more detail, or atleast point me in the right direction.
No problem Emil. Just contact me directly with your problem by selecting ‘Contact’ from the top menu.
Noticed in the exoplanet database that their is an excess of planets with orbital inclinations 90° why is this?
The orbital inclination is measured from the plan of the sky. Exoplanets which transit their host star at a ~90 degree angle from the plane of the sky. The excess of planets with high orbital inclinations is due to all the transiting planets which have been discovered.
Hi,
I am doing a simulator for the transit method in Python. I read that with the transit method we can obtain the radius of the planet and his density. Is there an equation to calculate the radius from the graph or the density?
It is true that you get the radius, but you not get the mass. To get the mass you need to use some other method such as the Radial Velocity method. Feel free to contact me directly if you still have any questions.
Hi Paul,
I’m trying to re-derive the transit duration and I agree totally with your expression. But the Winn textbook chapter you link to (and another paper, Seager & Mallen-Ornelas 2003) have a different expression for the transit duration with an additional factor of sin(i) in the denominator of the term within the arcsin. I can’t for the life of me figure out where that 1/sin(i) is coming from. Do you have any insight?
Hi Emily. At first glance I am not sure. Did you find an answer? I checked my derivation and it is correct.
Dear Paul & Emily:
I’ve been studying the exact same thing, and I believe I can answer Emily’s question. In Paul’s Fig. 3 above, the angle alpha is swept out from the star’s center (as seems reasonable). Therefore, the radius of the arc length swept out during the transit is just the semi-major axis, “a.” However, in the refs. to which Emily refers, I think the authors trace the points “A” and “B” in Fig. 3, not back to the star’s origin, but to a point on the “z-axis” (i.e., zero inclination), and the angle alpha is measured from that point. In that case, the radius is not “a”, but “a*sin(i)”. In the Seager & Mallen-Ornelas paper, this is written as a*sqrt(1 – cos^2(i)). This same technique is used to find an area (and volume) element in spherical coordinates, where the azimuthal arc length is expressed as “r*sin(theta)*d(phi)”. OK, having said all that, I’m still pondering which of the two origins is the more correct location from which to sweep out the angle alpha. These two methods clearly yield a different arc, but the corresponding chord–from which you derive the trig expression for transit time–seems identical.
I believe it comes down to whether you define your impact parameter, b, relative to ingress or relative to conjunction. The former will be slightly smaller than the latter, as for non-zero inclination the planet doesn’t trace a perfectly straight line across the star but instead arcs slightly towards the pole.
I’m not sure if there’s a correct choice, or even a convention – just something to bear in mind.
Hi,
I just wanted to say thank you for writing this – it was really helpful for my IB EE that I ended up getting top marks on.
Many thanks,
Max Nighswander
Thank you Max! It is kind of you to let me know. Makes me happy.
Hi there Paul
Thank you so much for this interesting article. A much nicer read than my text book! I really enjoyed it.
I noticed that in the caption of Fig.5 it says that orange is 1um. Is that right? I believe it should be something around 600nm ( 1000nm looks a bit too long to be in the visible spectrum).
Can you check that, please?
Kind regards
Javier
Hi Javier.
Yes, I believe 1 um is correct. CCD’s can still pick up this wavelength range, although they are typically not as sensitive in this region. In fact, your average digital camera is also sensitive to these wavelengths. Camera manufactures tend to put IR-blocking filters in though to give better colour rendition.
Hi Paul
Thanks for your prompt reply.
I understand that a CCD can detect photons beyond the human visible spectrum. My comment was about the wavelength of the orange colour which should be arund 600nm and not 1um (1000nm) as stated in the caption.
I hope this is clear now.
Kind regards
Javier
Hi Javier.
In the text under the figure I am referring to the colour of the lines used in the plot and not the colour of the actually light at a certain wavelength.
Hi Paul,
This is a great page, thanks for putting it out there – very useful.
Shaun
My pleasure Shaun.
Why is so important to re-determine the orbital parameters?.. The refinements are not really different to the ones that are calculated at the discovering. So is confusing to me.
Verification of results are an important part of science. Also, refined parameters are important to accurately determine parameters which may tell you a lot about the planet. For instance, an accurate radius and mass determination is vital if we wish to accurately calculate the average density (which may tell us something about the bulk composition of the planet). Accurate timing measurements may also tell us if there are other planets in the system etc.
Hi Paul, fascinating article. A very basic question: If you we comparing two light curves of two planets from the same system can you tell which planet is nearest to the star?
Yes Tony. The closer-in planet will have a shorter period (Kepler’s laws tells us this). Also the transit duration would be shorter for the closest planet (to the star), as it will move faster than a planet further out.
Great article. Can transit photometry be used to determine passing asteroids? Or are they too small? Also, would their trail have any effect on the observed transit curve?
Asteroids are too small to be detected using the transit method. Comets on the other hand are observed transiting distant stars. This is because various gasses sublimate from their surface as they approach the star which they orbit. This big cloud of gas obscures a significant fraction of the stellar disk. Have a look at the beta Pictoris system for more information.
Hi, can you tell me if there is any way to determine the semi-major axis of a transiting object from the light curve other than using Kepler’s Third Law?
Direct imaging I would assume, provided you have enough images of the planet to trace an orbit, it can be calculated geometrically.
Hello, I found this to be very useful as a student. Could you tell me what are the units of measurement for the transit duration formula? Thanks.
That will depend on what units you use for the Period. Typically I stick to the SI units and thus seconds.
Hello,
how can i calculate the radius of the planet ?
thaks
Using the first equation on the page, solve for Rp. So Rp = sqrt( delta F / F) * R*.
[…] orbiting around dwarf stars – like the Kepler and TESS missions. PLATO claims to be able to measure exoplanet radii from transits at a precision of 3%. This degree of precision would allow astronomers to answer many unsolved […]
You should take part in a contest for one of the highest quality blogs online.
I am going to highly recommend this website!
Hi, could you write the formula to obtain the inclination of an eccentric orbit? Or shall i get this value using the graph in figure 6? Also, why is phase unit in figure 6 expressed in days instead of degrees or radians?
Thanks a lot.
Hi Conchi. The equations on page two of this paper by Winn (2010) might help (https://arxiv.org/pdf/1001.2010v5.pdf). The exact equations you use depends on what you already know about the system. I would not read of figure 6 to get the values as this figure was made for a specific planet and star. Another star-planet combination would produce a difference dependence. It is the convention in exoplanet science to use the orbital phase as a unit for the x-axis, in my case I use days, but I could just as easily done it in hours. You can also use radians or degrees. What is important is that you state the units used.
Hi Paul, Amazing article. I wanted to know from where you took this data to plot a light curve and how did you corrected the raw data? Moreover, Could you tell me how the phase comes negative while plotting? I’m using Python to trying some plots.
[…] duration (tdur) should match the stellar density (ρs). There is a bit of weird geometry to do before it’s obvious why this is the case, but transit duration is proportional to the […]
[…] para detectar exoplanetas hasta la fecha. Esta entrada está inspirada en una del genial blog de Paul Anthony Wilson sobre tránsitos de exoplanetas. Del mismo modo, la mayoría de ecuaciones que se presentarán […]
[…] astronomical terms, “grazing” planets are defined as those that have an impact parameter that is larger than the planet-star radius ratio. The impact parameter is defined as the distance […]
[…] astronomical terms, “grazing” planets are defined as those that have an impact parameter that is larger than the ratio of the planet’s radius to the star’s radius. The impact parameter […]
[…] 1.15 Jupiter radii. You can read more about how planet radius, stellar radius and depth are related here. The equation I use here is a quicker method as the multiplication factor of 9.73 is such that if […]
hi paul, i don’t really get how to find i and it is needed to use any of the other formulas
[…] Puede leer más sobre cómo se relacionan el radio del planeta, el radio estelar y la profundidad aquí. La ecuación que uso aquí es un método más rápido ya que el factor de multiplicación de 9,73 […]
Hello,
Could you explain how excentricity of the orbit of the transiting planet affects the light curve, please?
Is it possible to see a change in ingress vs egress time due to the changing speed of the planet over the short time it spends transiting?
A good place to start might be Joshua Winn’s paper, which has equations which describe how the eccentricities affect the light curve: https://arxiv.org/pdf/1001.2010v5.pdf. To get a more practical feel for how it changes the light curve you could try and play around with: https://astro.unl.edu/naap/esp/animations/transitSimulator.html
Hello,
I’ve seen in the Internet that the flux can also be defined as proportional to (Area of the transiting object)^2 / (Area of the star)^2, instead of (Rp)^2 / (R*)^2. This formula is mainly used in technosignatures patterns prediction.
The problem is that I don’t understand how these two equations correlate, since (Area of the transiting object) = pi · Rp^2 and the same for the star radious, so the deduced formula would be ΔF ~ (Rp^2)^2 / (R*^2)^2, then ΔF ~ (Rp)^4 / (R*)^4
Could you explain why this is wrong? Thanks!
Hi Eric. Your first equation is wrong. It should be: “flux can also be defined as proportional to (Area of the transiting object) / (Area of the star)” so without the squares. The square term comes from the area. Thanks!
Hi, from some resources i learned that from transist method we can learn some features of the atmhosphere is there any article that i can read about?
Hi Paul,
Very nice post.
Should not be instead of sin(alpha/2)=l/a —> sin(alpha/2)=l/(a*sin i) ? This is what seems to me from the figure, and moreover with (a*sin i) in the denominator we recover the Eq. (3) of the paper
https://ui.adsabs.harvard.edu/abs/2003ApJ…585.1038S/abstract
for the duration of the transit
Many thanks
All the best
Vicent Martínez
If we took 1,000 average stars that have planets what percent of them would NOT be able to show planets using the transit method (even though it has planets) ?
ie. Looking at our SUNs north or south pole from 50 light years away would likely show ZERO planets and they might conclude no planets = no life = lets move on..